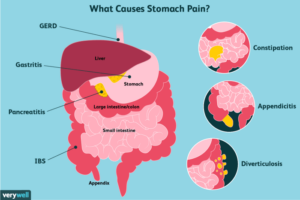
Srinivasa Ramanujan, the self-taught Indian mathematician who astounded the world with his extraordinary mathematical abilities, is known as “the man who knew infinity.” His groundbreaking discoveries in number theory, including the Ramanujan prime and modular equations, continue to shape modern mathematics.
Ramanujan’s journey from a humble background in India to the prestigious halls of Cambridge University is a testament to his brilliance and determination. Despite facing cultural differences and health challenges, he flourished under the mentorship of G.H. Hardy, who recognized his exceptional talent and guided his research.
Srinivasa Ramanujan’s Mathematical Genius: The Man Who Knew Infinity
Srinivasa Ramanujan was an Indian mathematician who lived in the early 20th century. He is considered one of the greatest mathematicians of all time, despite having no formal training in the subject. Ramanujan’s work has had a profound impact on number theory, analysis, and other areas of mathematics.One of Ramanujan’s most famous discoveries is the Ramanujan prime, which is a prime number that can be expressed as the sum of two cubes in two different ways.
He also discovered a number of modular equations, which are equations that relate the values of modular forms. These equations have applications in a variety of areas of mathematics, including number theory, physics, and cryptography.Ramanujan’s work was largely ignored by the mathematical community during his lifetime.
However, after his death in 1920, his work was rediscovered and has since been recognized as some of the most important mathematics of the 20th century.
Ramanujan’s Mathematical Abilities, The man who knew infinity
Ramanujan had an extraordinary ability to visualize mathematical concepts. He could see patterns and relationships in numbers that other mathematicians could not. He was also able to solve complex mathematical problems in his head, without using any written notes.Ramanujan’s mathematical abilities were not limited to number theory.
He also made important contributions to analysis, algebra, and other areas of mathematics. His work has had a profound impact on the development of mathematics in the 20th century and continues to be studied and admired by mathematicians today.
Ramanujan’s Discoveries in Number Theory
Ramanujan’s most famous discoveries in number theory include the Ramanujan prime and the modular equations. The Ramanujan prime is a prime number that can be expressed as the sum of two cubes in two different ways. The modular equations are equations that relate the values of modular forms.
These equations have applications in a variety of areas of mathematics, including number theory, physics, and cryptography.Ramanujan also made a number of other important discoveries in number theory. He discovered new formulas for pi, and he found new ways to solve Diophantine equations.
His work has had a profound impact on the development of number theory and continues to be studied and admired by mathematicians today.
Hardy’s Mentorship and Collaboration

Srinivasa Ramanujan’s extraordinary mathematical talent was recognized and nurtured by his mentor, G.H. Hardy, a renowned British mathematician at the University of Cambridge.
Hardy played a pivotal role in guiding Ramanujan’s research, providing him with invaluable advice and encouragement. He recognized Ramanujan’s exceptional abilities and saw the potential for groundbreaking discoveries. Hardy’s mentorship was instrumental in shaping Ramanujan’s mathematical journey and bringing his work to the forefront of the mathematical community.
Hardy’s Guidance
Hardy’s guidance was crucial in shaping Ramanujan’s mathematical development. He helped Ramanujan refine his ideas, provided constructive criticism, and suggested new avenues of exploration. Hardy recognized Ramanujan’s intuitive brilliance but also encouraged him to develop a more rigorous approach to his work.
- Hardy introduced Ramanujan to the Western mathematical literature, exposing him to a wealth of ideas and techniques.
- He guided Ramanujan in developing his own unique mathematical style, blending his intuitive insights with a more formal and structured approach.
- Hardy provided Ramanujan with a structured framework for his research, helping him to organize his ideas and focus his efforts on specific problems.
Promoting Ramanujan’s Work
Hardy was instrumental in promoting Ramanujan’s work and bringing it to the attention of the wider mathematical community. He published Ramanujan’s results in prestigious journals, organized conferences to showcase his work, and introduced him to other leading mathematicians.
- Hardy’s endorsement of Ramanujan’s work lent it credibility and helped to establish Ramanujan’s reputation as a mathematician of exceptional talent.
- Through his connections, Hardy facilitated collaborations between Ramanujan and other mathematicians, enabling Ramanujan to benefit from their insights and expertise.
- Hardy’s efforts helped to create a supportive environment for Ramanujan, fostering his growth and enabling him to make significant contributions to mathematics.
The Cambridge Experience
Upon arriving at Cambridge University in 1914, Srinivasa Ramanujan was a young man of extraordinary mathematical brilliance but limited formal education. He found himself immersed in a foreign culture and an unfamiliar academic environment.
Despite these challenges, Ramanujan’s mathematical genius quickly became apparent. He impressed renowned mathematicians like G.H. Hardy and J.E. Littlewood with his remarkable insights and unconventional approaches to problem-solving.
Cultural Differences and Health Issues
Ramanujan’s experience at Cambridge was not without its difficulties. He struggled to adapt to the cultural differences between India and England, particularly in terms of food, social customs, and the pace of life.
Moreover, Ramanujan’s health was often fragile. He suffered from a chronic illness that forced him to spend extended periods in a sanatorium. Despite these setbacks, he continued to produce groundbreaking mathematical work.
Collaboration with Other Mathematicians
Ramanujan’s collaboration with other mathematicians at Cambridge proved to be immensely fruitful. He worked closely with Littlewood and Watson, who helped him refine his ideas and develop new mathematical theories.
Together, they made significant contributions to number theory, partition theory, and other areas of mathematics. Ramanujan’s unique perspectives and innovative methods challenged established norms and inspired new lines of research.
Legacy and Impact
Srinivasa Ramanujan’s groundbreaking contributions to mathematics have left an enduring legacy, shaping the field and inspiring generations of mathematicians.
His work in number theory, in particular, has been immensely influential. Ramanujan’s ideas and discoveries have provided a foundation for modern number theory and continue to be a source of inspiration and research.
Ramanujan’s Influence on Number Theory
- Ramanujan’s work on modular forms, which are functions that are invariant under certain transformations, has had a profound impact on number theory. His discoveries in this area have led to the development of new theories and techniques, and have applications in various fields, including physics and cryptography.
- Ramanujan’s theory of partitions, which deals with the number of ways to represent a positive integer as a sum of smaller positive integers, has also been highly influential. His work in this area has led to new insights into the structure of numbers and has inspired further research in partition theory.
Ramanujan’s Impact Beyond Number Theory
- Ramanujan’s work has also had a significant impact on other fields of mathematics, including analysis, algebra, and combinatorics. His ideas have led to the development of new theories and techniques in these fields, and have inspired further research.
- Ramanujan’s work continues to be a source of inspiration for mathematicians today. His ideas and discoveries provide a foundation for further research and exploration, and his legacy continues to shape the field of mathematics.
Cultural and Historical Context
Srinivasa Ramanujan’s life and work were deeply shaped by the social and historical context of his time. Born in a small village in southern India in 1887, Ramanujan grew up in a traditional Hindu family. He displayed a remarkable aptitude for mathematics from an early age, but his formal education was limited due to financial constraints and the lack of opportunities for higher education in India at the time.
In 1914, Ramanujan sent a letter to the renowned British mathematician G.H. Hardy, who was immediately impressed by Ramanujan’s raw talent. Hardy invited Ramanujan to come to Cambridge, England, where he could further his mathematical studies. Ramanujan’s arrival in Cambridge in 1914 marked the beginning of a remarkable collaboration between the two mathematicians.
Challenges Faced by Ramanujan
As an Indian mathematician working in early 20th-century Britain, Ramanujan faced a number of challenges. He came from a culture that was very different from the Western academic world, and he had to adapt to a new language, a new way of life, and a new way of doing mathematics.
Additionally, Ramanujan was a devout Hindu, and he faced some prejudice from his British colleagues who did not understand his religious beliefs.
Despite these challenges, Ramanujan’s mathematical genius shone through. He made significant contributions to number theory, analysis, and other areas of mathematics. He published over 30 papers in his lifetime, and his work has had a lasting impact on the field of mathematics.
Concluding Remarks
Ramanujan’s legacy extends far beyond his short life. His work has had a profound impact on number theory, analysis, and other fields of mathematics. His ideas continue to inspire mathematicians and scientists around the world, ensuring that his legacy as “the man who knew infinity” will endure for generations to come.